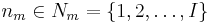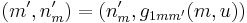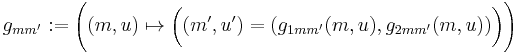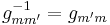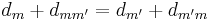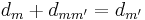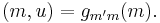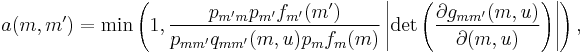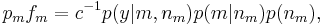Reversible-jump Markov chain Monte Carlo
In computational statistics, reversible-jump Markov chain Monte Carlo is an extension to standard Markov chain Monte Carlo (MCMC) methodology that allows simulation of the posterior distribution on spaces of varying dimensions.[1] Thus, the simulation is possible even if the number of parameters in the model is not known.
Let
be a model indicator and 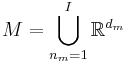 the parameter space whose number of dimensions
the parameter space whose number of dimensions 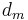 depends on the model
depends on the model 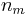 . The model indication need not be finite. The stationary distribution is the joint posterior distribution of
. The model indication need not be finite. The stationary distribution is the joint posterior distribution of 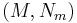 that takes the values
that takes the values 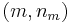 .
.
The proposal 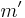 can be constructed with a mapping
can be constructed with a mapping 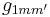 of
of  and
and  , where
, where  is drawn from a random component
is drawn from a random component  with density
with density  on
on 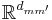 . The move to state
. The move to state 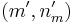 can thus be formulated as
can thus be formulated as
The function
must be one to one and differentiable, and have a non-zero support:
so that there exists an inverse function
that is differentiable. Therefore, the 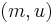 and
and 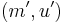 must be of equal dimension, which is the case if the dimension criterion
must be of equal dimension, which is the case if the dimension criterion
is met where 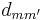 is the dimension of
is the dimension of  . This is known as dimension matching.
. This is known as dimension matching.
If 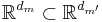 then the dimensional matching condition can be reduced to
then the dimensional matching condition can be reduced to
with
The acceptance probability will be given by
where  denotes the absolute value and
denotes the absolute value and 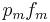 is the joint posterior probability
is the joint posterior probability
where  is the normalising constant.
is the normalising constant.
References
- ^ Green, P.J. (1995). "Reversible Jump Markov Chain Monte Carlo Computation and Bayesian Model Determination". Biometrika 82 (4): 711–732. doi:10.1093/biomet/82.4.711. JSTOR 2337340. MR1380810.